Learn123

Exam Questions - Walkthrough

June 2005 C1 OCR MEI

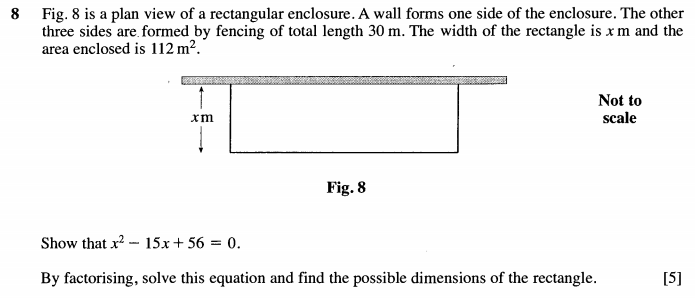
As this is solving by 'factorising' we just need to learn the methods we've learnt to find two different solutions. So we need to find two numbers that add together to make -15 and multiply to give 56. The only numbers for this are 8 and 7.

(x - 7)(x - 8)

This means that x = 7 or 8. Lets try 7 first...

2 × 7 = 14
30 - 14 = 16
16 × 7 = 112m²

As this fits the question, x = 7 and the dimensions of the rectangle are 7m × 16m.

January 2007 C1 OCR MEI

We're going to add a +0 into the first equation to make it easier to use the method we've learnt...

x² + 0x - 4

So, we need to find two numbers that multiply to give -4 and add to give 0. This is -2 and +2. Now we've got our first factorised equation - (x - 2)(x + 2).

The next one is going to be worked out the same way.

x² - 5x + 6

We need two numbers that multiple to give 6 and add to give -5. This is -2 and -3.

(x - 2)(x - 3)

So as a fraction, this is: ^{(x - 2)(x + 2)} ⁄ _{(x - 2)(x - 3)}

But, we can simply that further by looking for things that can be cancelled top and bottom. This is (x - 2):

^{(x + 2)} ⁄ _{(x - 3)}

January 2008 C1 OCR MEI

We're going to do each side of the fraction separate, so lets do the bottom one first, as it's easier and there's only one answer to it - as we can use one of the brackets to work out what the other one is. Also, we need to simplify later on so we need one of the factors to cancel out. We're going to add a +0 into the middle of the equation to make it easier to use the method we've learnt.

x² + 0x - 1

We need two numbers that multiply to give -1 and add to give 0. This could be -1 and +1.

(x - 1)(x + 1)

Now we need to find something in brackets that multiplies either (x - 1) or (x + 1) to give the equation below.

3x² - 7x + 4

We know one of them has to be 3x to get the first term, so lets put that in as the first term in the bracket. Now our factorised equation could be either(3x +/- ?)(x - 1) or (3x +/- ?)(x + 1).
By trial and error, let's try to find the missing number that will multiply to give +4.
It can only be either -2 and -2, +2 and +2, -4 and -1 or +4 and +1... but we already know that it's either +1 or -1, so it has to be either +4 or -4.
(3x + 4)(x + 1) = 3x² + 4x + 3x + 4 = 3x² + 7x + 4
(3x - 4)(x - 1) = 3x² - 4x - 3x + 4 = 3x² - 7x + 4 ✓

So the fraction looks like this:

^{(3x - 4)(x - 1)} ⁄ _{(x - 1)(x + 1)}
^{(3x - 4)} ⁄ _{(x + 1)}