January 2008 - Question 3



For this question, it may help you to draw a tree diagram

As the question is asking about the probability of something AND something happening, we need to times the two values together.
First, we need to get the probability of Steve not being delayed on the way home. To do this, we simply need to subtract the probability that he is delayed on the return flight from 1.
1 - 0.2 = 0.8
So now all we need to do is times them together:
0.3 × 0.8 = 0.24




As these events are mutually exclusive from each other, we need to work out P(A∪B) which gives us P(A) + P(B).
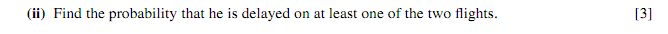
Let's look at the different ways he could be delayed at least once...

Delayed & delayed = 0.3 × 0.2 = 0.06
Delayed & not delayed = 0.3 × 0.8 = 0.24
Not delayed & delayed = 0.7 × 0.2 = 0.14

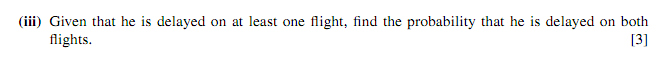
Then we just need to add these together...

0.06 + 0.24 + 0.14 = 0.44




This is conditional probability - the probability of something, given that something else has already happened.
For example, P(B|A) means the probability of B, given that A has already happened.
The formula for this is...

P(B|A) = P(A∩B) / P(A)


First, lets work out P(A∩B).

P(A∩B) = 0.3 × 0.2 = 0.06


The P(A) was worked out earlier in part (ii), so it's 0.44. Now let's work out the formula...

0.06 / 0.44 = 6/44 = 0.136

Bookmark and Share