January 2008 - Question 7



For this we need to use binomial distribution as we need to find out the certain number of 'successes' in a fixed number when there's only two outcomes and each trial is independent of each other.

If random variable X has a binomial distribution, then the formula will be X ~ B(n, p)


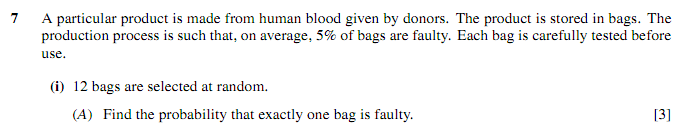
The probability that X is a certain value (like in this question, it's 1) is:

P(X = x) = (n! / x!(n - x))pxqn-x where q = 1 - p


We're going to let X be the random variable "number of faulty bags". Here, n = 12 (because 12 bags are selected so there will be 12 trials). P = 0.05 because of the 5% probability that the bag is faulty, so q = 1 - 0.05 = 0.95. This means that X ~ B(12, 0.95).
Now we're going to calculate the probability of 1 'success', i.e. X = 1.

P(X = 1) = 12! / 1!(12 - 1) × 0.051 × 0.9511
P(X = 1) = 12 × 0.05 × 0.568800092
P(X = 1) = 0.3413 (4 s.f.)




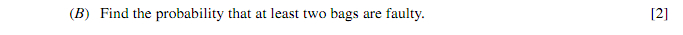
For this, we want to see the probability for 2 bags or more to be faulty.

P(X ≥ 2) = 1 - P(X ≤ 2)
P(X = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or 12) = 1 - P(X = 0 or 1)

To find P(X = 0 or 1), we need to look at the statistical tables that you'll get with your exam paper.
Find the row n = 12, as we're picking 12 bags. Then look at x = 1, as the highest amount X can equal is 1. We're already told what p is - 0.05, so we need to look at that column. You should get 0.8816.

1 - 0.8816 = 0.1184




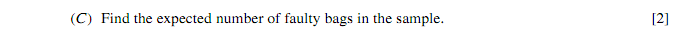
This question is much easier than it sounds. For a binomial distribution, the mean or expected value is...

E(X) = np


As n = 12 and p = 0.05, we just need to multiply them together to get the answer.

E(X) = 12 × 0.05 = 0.6


Bookmark and Share